Prove that (ab/bc) = (ad/dc). Examples on internal and external angle bisector theorem solution :.
Exterior Angle Bisector Theorem, Angle bisector theorem when the side lengths and angle bisector is known, angle bisector theorem can be applied then. This product is included for free in the trian. According to heath (1956 , p.

Here de is the internal angle bisector of angle d. The triangle angle bisector theorem states that in a triangle, the angle bisector of any angle will divide the opposite side in the ratio of the sides containing the angle.consider the figure below: Likewise, there is an exterior angle bisector that is defined as a line or line segment that which divides into. External angle bisector theorem :
###External Bisector of angle of triangle divides opposite To bisect an angle means to cut it into two equal parts or angles.

Teorema de la bisectriz de ángulo Angle bisector theorem, Examples on internal and external angle bisector theorem solution :. An angle bisector is a line or ray that divides an angle in a triangle into two equal measures. In a quadrilateral abcd, the bisectors of ∠b and ∠d intersect on ac at e. The exterior angle is equal to the sum of the two remote interior angles. The triangle.
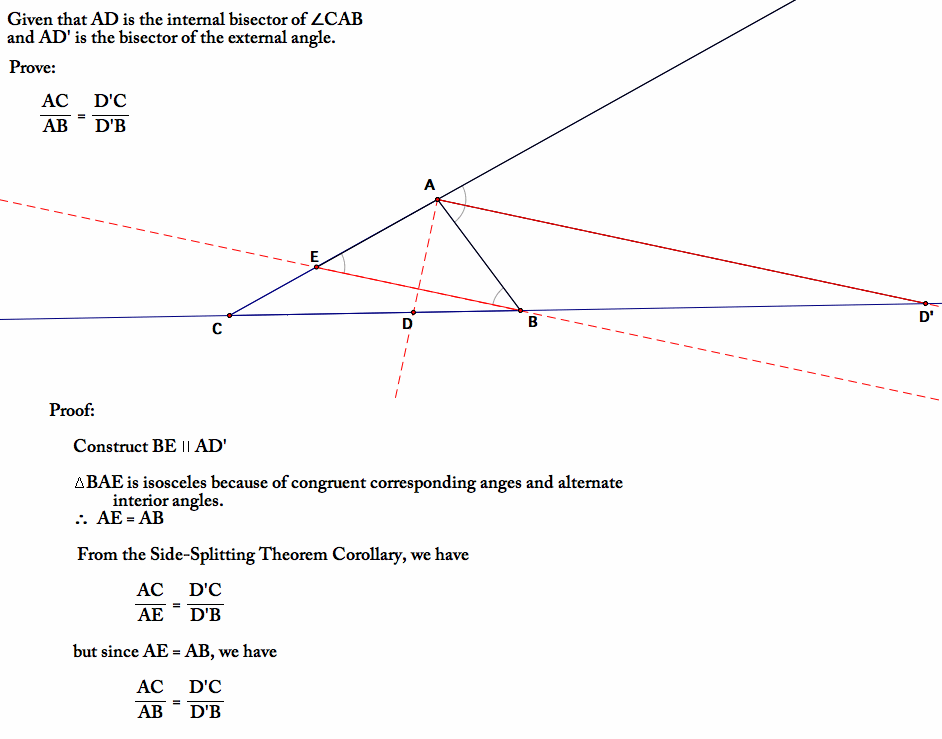
Section 4.2 Discussion, The exterior angles, taken one at each vertex, always sum up to 360°. This is a coloring activity for a set of 12 problems on the exterior angle sum theorem. You have to use both. The external bisector of an angle of a triangle divides. An angle bisector is a line or ray that divides an angle in a triangle.
Chapter 5 Review Perpendicular Bisector, Angle Bisector, The angle bisector defined above is the interior angle bisector. We recall the theorems regarding the ratio of line segments related to the interior and exterior angle bisectors of a triangle. About press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features press copyright contact us creators. Prove that (ab/bc) = (ad/dc)..
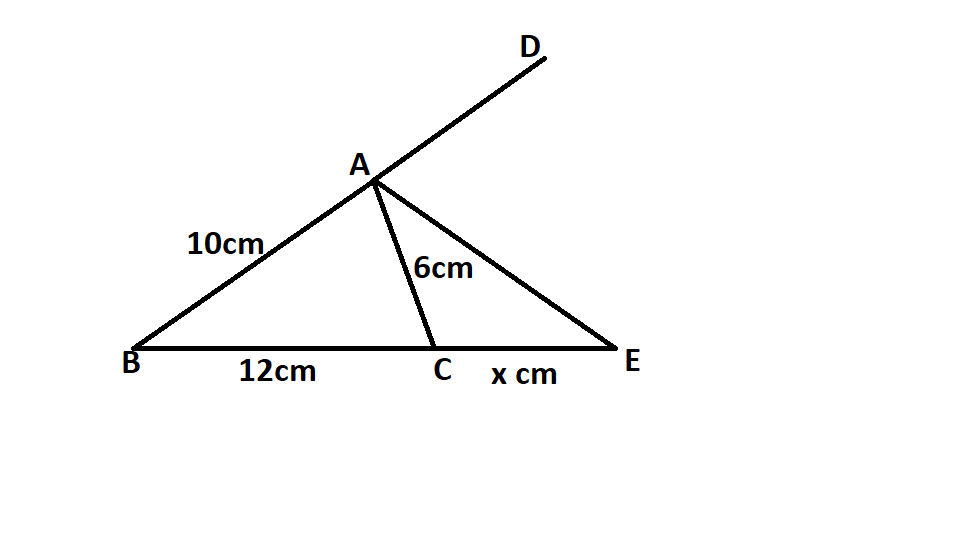
In the given figure AE is the bisector of the exterior, Angle bisector theorem has further established the derivation of this concept. An angle bisector is a line or ray that divides an angle in a triangle into two equal measures. 2)), the corresponding statement for an external angle bisector was given by robert simson who noted that pappus assumed this result without proof. Angle bisector theorem when the side lengths.

External Angle bisector Theorem of triangle External, The internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding sides containing the angle. Angle bisector theorem when the side lengths and angle bisector is known, angle bisector theorem can be applied then. In geometry, the angle bisector theoremis concerned with the relative lengthsof the two segments that.

The external angle bisector of an angle of a triangle, We recall the theorems regarding the ratio of line segments related to the interior and exterior angle bisectors of a triangle. Angle bisector theorem when the side lengths and angle bisector is known, angle bisector theorem can be applied then. According to the angle bisector theorem, a triangle abc, a line bisects the side bc at point d. The angle.

Exterior angle bisector theorem YouTube, The angle bisector defined above is the interior angle bisector. The exterior angle is equal to the sum of the two remote interior angles. 2)), the corresponding statement for an external angle bisector was given by robert simson who noted that pappus assumed this result without proof. Here be is the internal angle bisector of angle b. In δabc, ad.

Lesson Video Angle Bisector Theorem and Its Converse Nagwa, It equates their relative lengths to the relative lengths of the other two sides of the triangle. According to the angle bisector theorem, a triangle abc, a line bisects the side bc at point d. The triangle angle bisector theorem states that in a triangle, the angle bisector of any angle will divide the opposite side in the ratio of.

Exterior angle bisector theorem proof YouTube, This is a coloring activity for a set of 12 problems on the exterior angle sum theorem. According to heath (1956 , p. Here be is the internal angle bisector of angle b. You have to use both. The measure of exterior angle = sum of two opposite interior angles’ measure what is the exterior angle inequality theorem?

External Bisector of angle of triangle divides opposite, Prove that (ab/bc) = (ad/dc). Here de is the internal angle bisector of angle d. Here be is the internal angle bisector of angle b. An angle bisector is a line or ray that divides an angle in a triangle into two equal measures. The measure of exterior angle = sum of two opposite interior angles’ measure what is the.
Exterior Angle Bisector of Triangle Dividing Opposite Side, Angle bisector theorem has further established the derivation of this concept. Angle bisector theorem when the side lengths and angle bisector is known, angle bisector theorem can be applied then. 𝐷 𝐶 𝐷 𝐵 = 𝐴 𝐶 𝐴 𝐵, 𝐸 𝐵 𝐸 𝐶 = 𝐴 𝐵 𝐴 𝐶. According to the angle bisector theorem, a triangle abc, a line bisects.

Pin on exterior angle theorem calculator, Angle bisector theorem when the side lengths and angle bisector is known, angle bisector theorem can be applied then. Here be is the internal angle bisector of angle b. This product is included for free in the trian. Subtract the sum of the two angles from 180 to find the measure of the indicated interior angle in each triangle. An.

Angle Bisector Theorem Intro YouTube, External angle bisector theorem : We recall the theorems regarding the ratio of line segments related to the interior and exterior angle bisectors of a triangle. 𝐷 𝐶 𝐷 𝐵 = 𝐴 𝐶 𝐴 𝐵, 𝐸 𝐵 𝐸 𝐶 = 𝐴 𝐵 𝐴 𝐶. The external bisector of an angle of a triangle divides. Likewise, there is an exterior angle.

Proof Exterior Angle Bisector Theorem. triangle angle, 2)), the corresponding statement for an external angle bisector was given by robert simson who noted that pappus assumed this result without proof. Here, ps is the bisector of ∠p. Likewise, there is an exterior angle bisector that is defined as a line or line segment that which divides into. In the case of a triangle, the bisector of the.
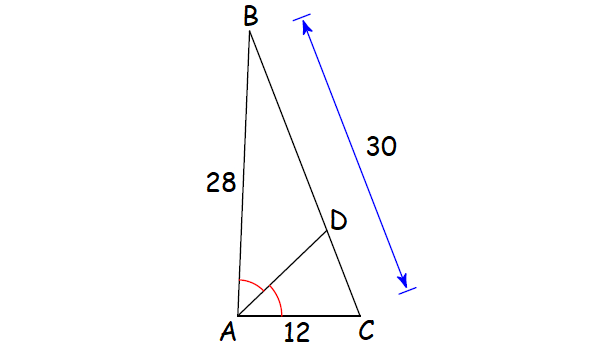
Angle bisector theorem proof, 𝐷 𝐶 𝐷 𝐵 = 𝐴 𝐶 𝐴 𝐵, 𝐸 𝐵 𝐸 𝐶 = 𝐴 𝐵 𝐴 𝐶. The angle bisector theorem is concerned with the relative lengths of the two segments that a triangle�s side is divided into by a line that bisects the opposite angle. The angle bisector defined above is the interior angle bisector. The measure of.
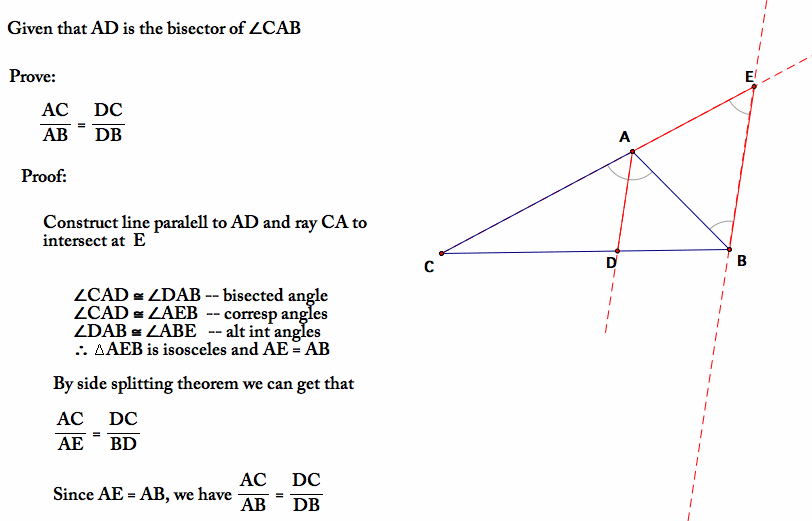
Section 4.2 Discussion, In δabc, ad is the internal bisector of ∠bac which meets bc at d. It equates their relative lengths to the relative lengths of the other two sides of the triangle. Prove that (ab/bc) = (ad/dc). Here be is the internal angle bisector of angle b. The angle bisector defined above is the interior angle bisector.
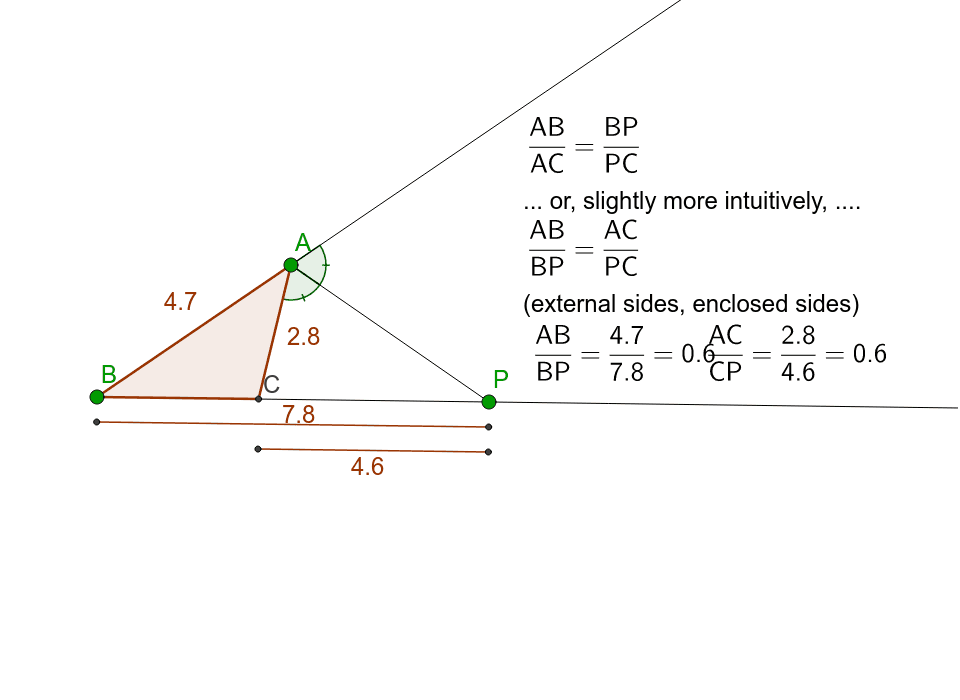
Angle bisector theorem (external) GeoGebra, It equates their relative lengths to the relative lengths of the other two sides of the triangle. The internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding sides containing the angle. 2)), the corresponding statement for an external angle bisector was given by robert simson who noted that.
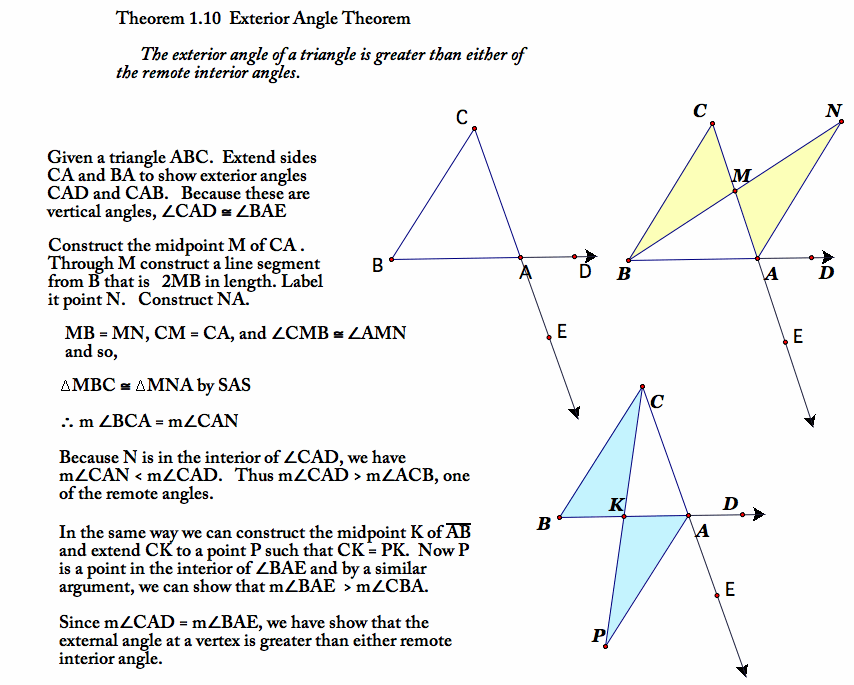
Section 1.2, This is a coloring activity for a set of 12 problems on the exterior angle sum theorem. According to the exterior angle inequality theorem, the measure of an exterior angle of a triangle is greater than either of its interior opposite angles. Examples on internal and external angle bisector theorem solution :. This product is included for free in the.

Internal Angle Bisector Theorem of Triangle Internal, Subtract the sum of the two angles from 180 to find the measure of the indicated interior angle in each triangle. An exterior angle is supplementary to its adjacent triangle interior angle. Likewise, there is an exterior angle bisector that is defined as a line or line segment that which divides into. The exterior angles, taken one at each vertex,.

5.3 Angle Bisectors Theorems YouTube, Here, ps is the bisector of ∠p. The theorems tell us the following identities: According to the angle bisector theorem, a triangle abc, a line bisects the side bc at point d. Examples on internal and external angle bisector theorem solution :. The explanation of this theorem is discussed ahead.








